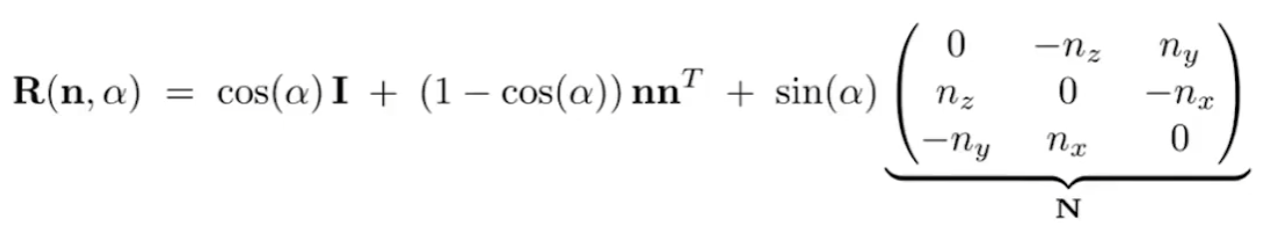写shader对线性代数的要求还是挺高的w…毕竟基础原理和线代密切相关，主要是矩阵和矩阵变换那块的内容，现在来复习一下!

坐标系

为了给每个点一个确切的表示，我们规定一个坐标系。坐标系基于一个人为规定的原点，以及相互垂直的坐标轴。二维的笛卡尔坐标系属于小学生都会的范畴就不多提了，三维笛卡尔坐标系由于镜面对称(像手性碳一样)分为两种：左手系和右手系。
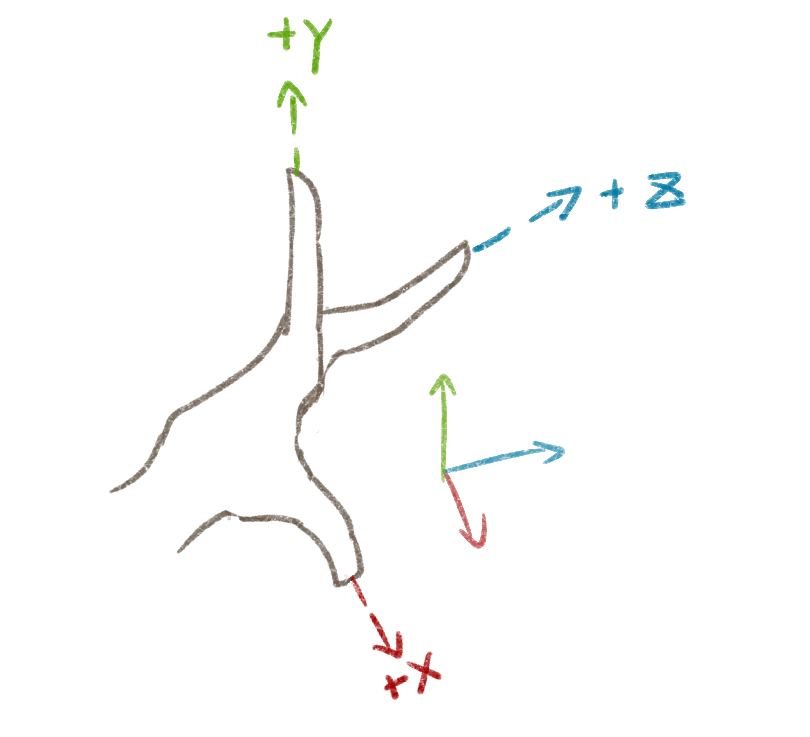
如何区分左手系和右手系？习惯上，我们用：

拇指表示x轴正方向
食指表示y轴正方向
中指表示z轴正方向

很明显，用左手和右手都可以获得一个三维笛卡尔坐标系，它们镜面对称从而不完全一样，于是我们把左手表示的坐标系称为左手系，右手的称为右手系。Unity和Blender使用的都是左手系。
那么这两种手系可以互相转换吗？答案当然是可以，只需要把左手系的一根坐标轴的方向反过来它就变成了右手系，对于右手系也是同理。这也是为什么从摄像机角度出发的观察空间(View Space)是右手系，因为摄像机出发的前向的z轴是负方向。

不同手系的正向旋转
不同手系的正向旋转完全不同，不过我们可以用手性法则来表示不同手系的正向旋转！
由此，左手法则表示的旋转方向就是左手系的正向旋转方向；右手法则表示的旋转方向就是右手系的正向旋转方向

向量

向量(通常用粗体小写字母 $\textbf{a}, \textbf{b}, \textbf{u}$ 等表示)在物理中又被称作矢量，就是有模长(mganitude)和方向(direction)的量，我们一般用 $\textbf{v}=(x, y)$ 来表示二维矢量，用 $\textbf{v}=(x, y, z)$ 来表示三维矢量，用 $\textbf{v}=(x, y, z, w)$ 来表示四维矢量

加、减、标量乘除

当我们进行向量与标量的乘除法、向量间的加减法时我们需要注意这些操作体现出来的几何意义。
向量的加减法遵循三角形定则(triangle rule):

而标量与向量的乘除则直接放缩了原本的向量：

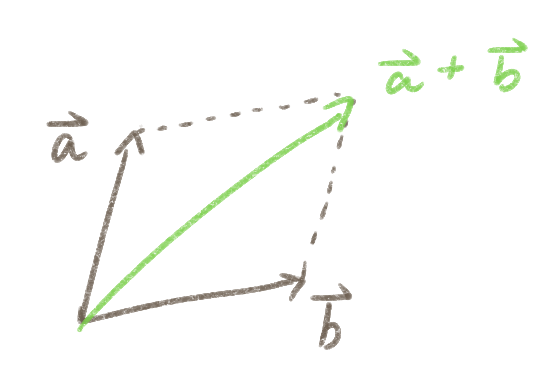
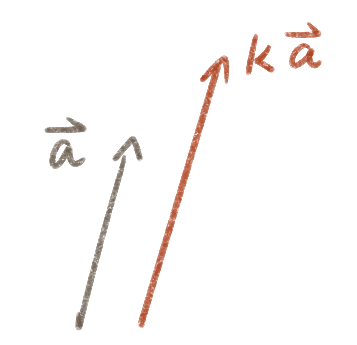
点乘和叉乘

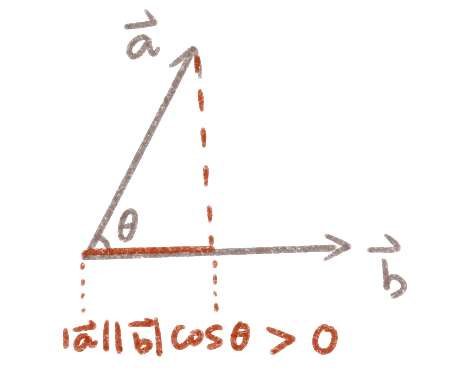
向量之间的点乘( $\textbf{a} \cdot \textbf{b} = |a||b|cos\theta$ ,结果将得到一个标量 )存在一种投影关系:

当a与b垂直时，投影长度为0，a与b点乘的结果为0
当我们知道坐标时，可以有(x1, y1, z1) · (x2, y2, z2) = x1x2 + y1y2 + z1z2
点乘的运算顺序优先于乘法和除法

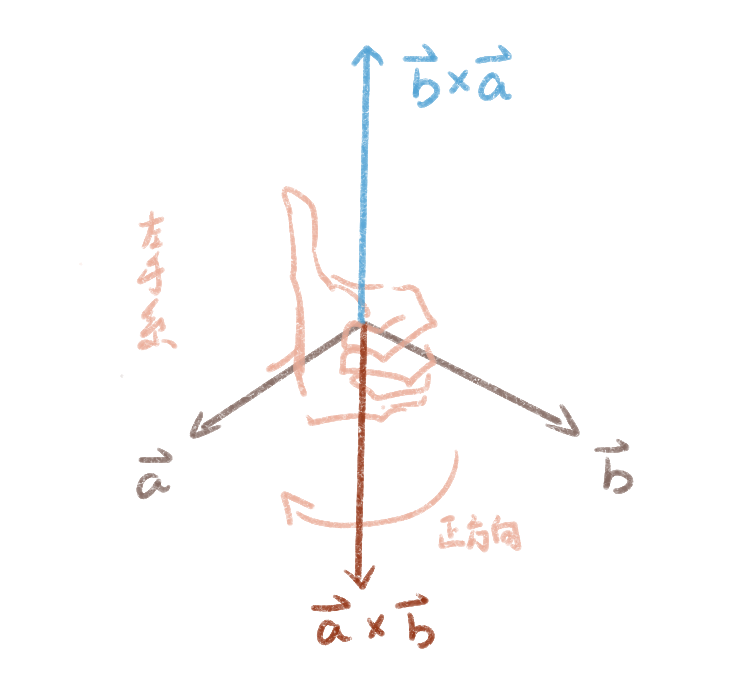
向量之间的叉乘( $\textbf{a} \times \textbf{b} = |a||b|sin\theta$ ,结果将得到一个矢量 )，其结果垂直于两个原向量所构成的平面:

点乘不考虑顺序问题，但叉乘考虑。不同的顺序会得到方向不同的结果，如右图---->
左手系中判断叉乘结果的方向使用左手法则；右手系则使用右手法则
当我们知道坐标时，可以有(x1, y1, z1) · (x2, y2, z2) = (y1z2-z1y2, x1z2-z1x2, x1y2-y1x2)
当a和b平行，即 $sin\theta = 0$ ，我们将得到一个零向量

叉乘的应用
我们通过片元上顶点是顺时针还是逆时针来判断这个片元是正对我们的还是背对我们的。可以利用叉乘带来的方向来判断三角形的三个顶点是顺时针还是逆时针

矩阵

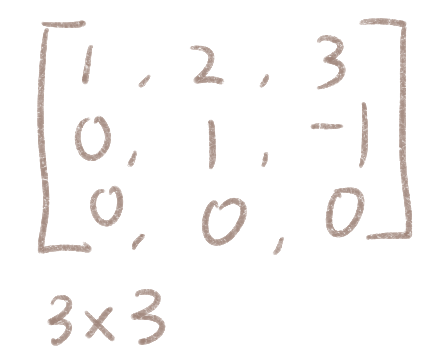
矩阵就是像这样由行和列组成的一组数据，本质上也是数组，不过是二维的。右图是一个3*3的方矩阵，矩阵的行和宽可以是0，这时候就变成了一维的行矩阵、列矩阵或者什么都没有的0矩阵了。
我们一般用m[i][j]来表示第i行j列的矩阵元素

标量乘除

同样的，我们在进行矩阵运算的时候也要考虑其中的几何意义。
矩阵与标量的乘除法相当于整体扩充或者缩小的矩阵，我们将矩阵的每个元素都乘上/除以标量

矩阵乘法

矩阵与矩阵相乘必须满足笑脸定律，也就是仅m * n的矩阵和n* k的矩阵能够相乘，最后得到一个m * k的矩阵。m和k的值可以相同。矩阵乘法的示意图如下：

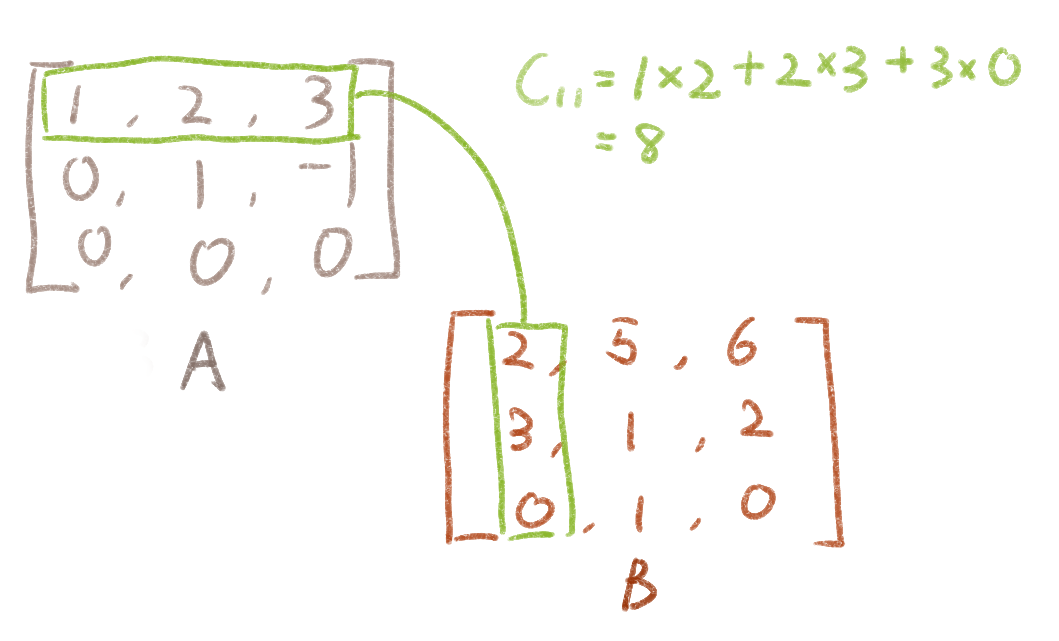
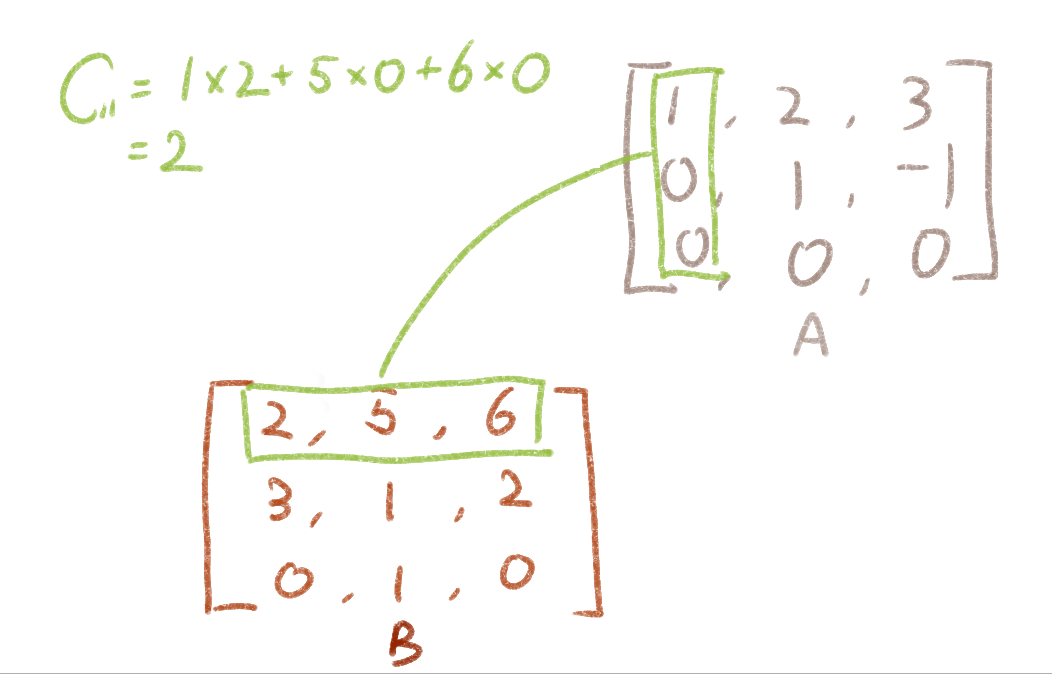
左图表示AB，而右图是BA
于是你也发现了，矩阵乘法的这种性质决定了更改乘法的顺序就会得到灾难性的结果。但在不改变左右顺序的情况下，我们先计算拿两个矩阵相乘是不影响最终结果的，也就是说：ABCDEF = A((BC)E)F

有关矩阵运算、矩阵类型等等更多的内容，可以看EE112下的笔记

矩阵变换(Transform)

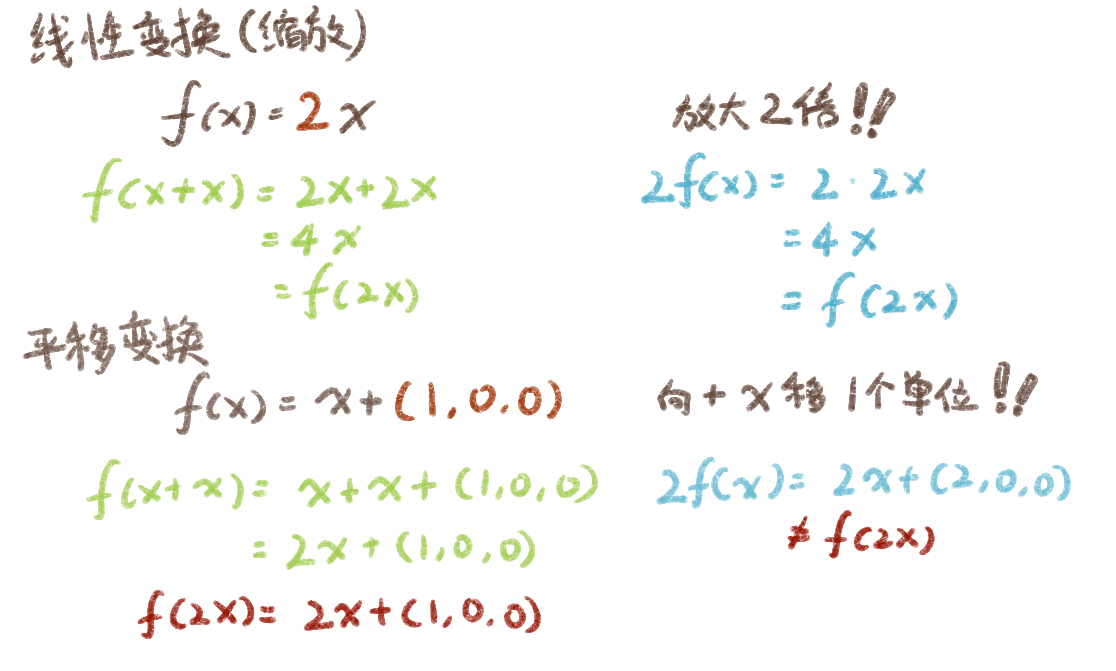
矩阵变换一般包括缩放、平移和旋转。我们用某个点或者矢量使用特定的变换矩阵，就能得到变换后新的点或矢量。最常见的应用例子就是顶点着色器中将应用传输进来的模型空间的顶点坐标经过MVP矩阵的变换转变成裁剪空间中的坐标。
变换包括线性变换和平移变换。其中：

线性变换包括缩放、旋转、错切、镜像和正交投影
线性变换满足f(x) + f(y) = f(x+y)和kf(x) = f(kx)
平移变换不满足线性加法和线性乘法

如右图所示，线性变化（以缩放为例）满足线性加法（左）和线性乘法（右），而平移变换则不满足。当给予x一个确定的值，如（1，1，2）时将会明显的发现获得的结果不满足线性乘法。所以为了统一线性变换和平移变换，我们采用四维空间(齐次坐标空间)下的仿射变换进行矩阵变换操作。而转换到齐次空间之后的点和向量的坐标就是齐次坐标(homogeneous coordinate)。
一般的，我们有如下规则：

点的齐次坐标的w分量为1
向量的齐次坐标的w分量为0（目的是不受平移影响，因为位置对于向量来说并不重要）

平移矩阵

从上文的内容中我们得知，平移并不是线性变换，而是仿射变换。为了统一仿射变换和线性变换我们才需要齐次坐标。很基本的原因是：我们没有办法在同一个维度中简单的用一个变换矩阵和点/向量相乘得到平移后的结果。
比如说：

\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax + by \\ cx + dy \end{pmatrix}

我们如果我们要把图形所以的点向左平移一个单位，那么我们得到的结果的矩阵应该是 $\begin{pmatrix} x+1\\ y\end{pmatrix}$ 。啊，但是我们刚刚得到的公式好像并没有办法加上常数。所以，想要在同一个维度中得到正确的平移变换，我们需要稍微修改一下这个公式，得到：

\begin{pmatrix} x' \\ y' \end{pmatrix}= \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} t_{x} \\ t_{y} \end{pmatrix}

于是， $x' = ax + by + t_{x}$ ，我们甚至可以把abcd转变成 $I$ 矩阵的形式，因为没有必要弄的这么复杂，直接每个坐标轴移动多少加上去就好了。但是仿射变换的小尾巴无法和线性变换统一，而加上一个维度就能解决不统一的问题，何乐而不为呢？于是，在齐次坐标空间下，平移变换的变换矩阵可以简化为：

\begin{pmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + t_{x} \\ y + t_{y} \\ z + t_{z} \\ 1 \end{pmatrix}

于是乎，一个点经过平移矩阵 $\begin{pmatrix}1& 0& 0& t_{x} \\ 0& 1& 0& t_{y} \\ 0 & 0& 1& t_{z} \\ 0& 0& 0& 1\end{pmatrix}$ 变换之后得到的结果就是该点在空间中平移了 $(t_{x}, t_{y}, t_{z})$ 之后的结果。
但是如果我们对一个向量的齐次坐标进行同样的平移操作，我们会得到：

\begin{pmatrix} 1 & 0 & 0 & t_{x} \\ 0 & 1 & 0 & t_{y} \\ 0 & 0 & 1 & t_{z} \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 0 \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \\ 0 \end{pmatrix}

发现平移对向量没有任何影响。原因在上文中提到过了

镜像矩阵

我们需要考虑针对哪条轴进行镜像（就是对称）操作。举个例子，一个点 $(x, y, z)$ 和x轴镜像的点的坐标为 $(-x, y, z)$ 。如果镜像的轴并不是坐标轴那么变换会变得更复杂，涉及到复合变换。
对x轴的镜像变换操作为：

\begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} -x \\ y \\ z \\ 1 \end{pmatrix}

易得，对y轴进行镜像即将变换矩阵的矩阵元素 $M_{2,2}$ 改为-1，而其他对角元素保持为1不变即可。z轴镜像类似

错切矩阵

错切这个词听起来比较陌生，似乎我们日常生活中不怎么接触到这个操作。实际上错切用通俗的话来讲就是拽着一条边拉动，比如下图的两种都是错切：

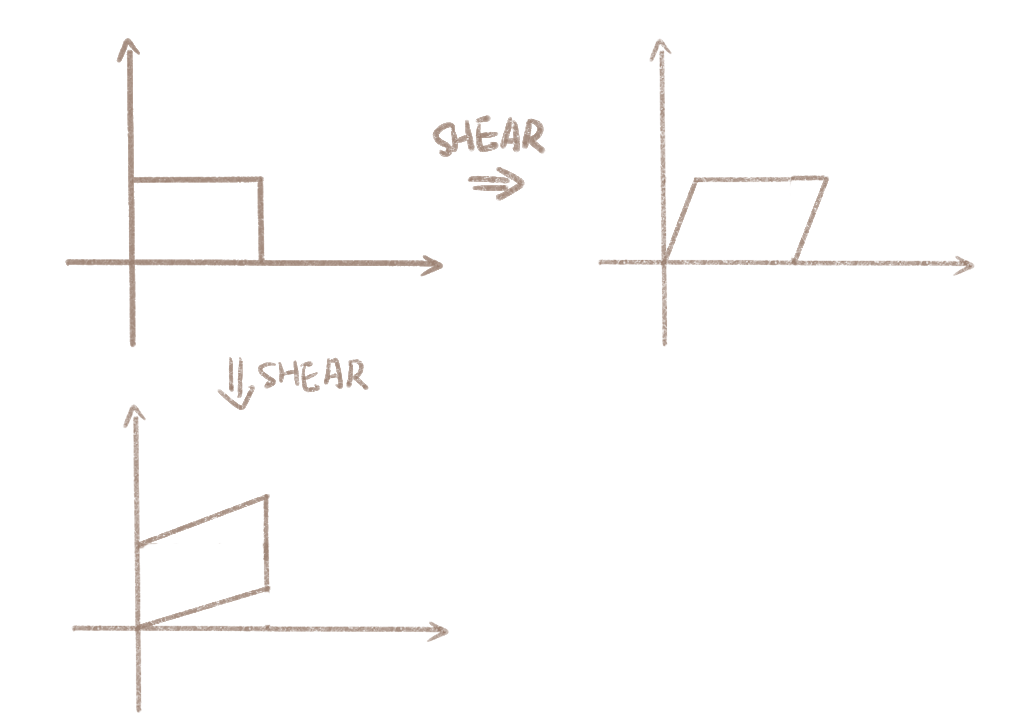
我们要如何表示错切呢？首先找到不变的轴。比如右图上方的情况，我们发现图形在变换过程中每个点的纵坐标都没有改变。接下来我们观察每个点的横坐标，发现y = 0时物体的横坐标不变，y = 1时（假定经过错切变换后的图形纵坐标最大为1）所有点的横坐标都向右偏移了a个单位。不难发现，随着点的纵坐标不断变大，点横坐标的偏移不断线性地变大，直到达到a。
如果变化不是线性的呢？那么非线性的变化会体现在图形的边上。当然，这样的变换也不能称之为“错切”了。
以三维笛卡尔坐标系为例，沿x轴水平错切的变换矩阵公式为（错切斜率为1/m）：

\begin{pmatrix} 1 & m & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + my \\ y \\ z \\ 1 \end{pmatrix}

缩放矩阵

\begin{pmatrix} k_{x} & 0 & 0 & 0 \\ 0 & k_{y} & 0 & 0 \\ 0 & 0 & k_{z} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} k_{x}x \\ k_{y}y \\ k_{z}z \\ 1 \end{pmatrix}

可以看到，缩放矩阵成功的让点的齐次坐标沿坐标轴产生了缩放。这对向量坐标同样有用：

\begin{pmatrix} k_{x} & 0 & 0 & 0 \\ 0 & k_{y} & 0 & 0 \\ 0 & 0 & k_{z} & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 0 \end{pmatrix} = \begin{pmatrix} k_{x}x \\ k_{y}y \\ k_{z}z \\ 0 \end{pmatrix}

当 $k_{x}, k_{y}, k_{z}$ 的值一样时，这种类型的缩放被称为统一缩放(uniform scale)，否则则被称为非统一缩放。统一缩放能够在各方向上均匀的“缩放原物体，而非统一缩放会产生“拉伸”的效果。

旋转矩阵

旋转矩阵比前两种要复杂一些。因为我们要考虑点/向量是围绕哪个坐标轴进行旋转的（如果不是围绕xyz轴旋转则更复杂，需要使用复合矩阵）。以围绕x轴旋转 $\theta$ 度为例的旋转矩阵为：

R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta& -sin\theta& 0 \\ 0 & sin\theta& cos\theta& 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

绕y轴旋转的旋转矩阵则为：

R_{y}(\theta) = \begin{pmatrix} cos\theta & 0 & sin\theta& 0 \\ 0 & 1 & 0 & 0 \\ -sin\theta& 0 & cos\theta& 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

最后，绕z轴旋转的旋转矩阵为：

R_{z}(\theta) = \begin{pmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta & cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}

罗德里格斯旋转公式(Rodrigues’ Rotation Formula)
啊，好高级的名字！前面我们提到的旋转矩阵只能沿坐标轴旋转，这也太拉了，那这个公式就是用来解决沿任意轴进行旋转的问题的。罗德里格斯旋转公式如下：

首先我们需要知道旋转的轴n和旋转的角度α。轴和向量并不等同，因为向量没有位置的属性，而轴有。在这个公式中，我们默认轴指的是从原点出发的轴。有人会问，那像x = 3这样的轴要怎么表示呢？它不过原点。解决方法是：

先把旋转中心移动到经过原点（x = 3 —> x = 0），需要旋转的点/向量也会相应的被移动。所以，首先我们需要乘上一个平移矩阵

代入罗德里格斯旋转公式进行旋转

再将旋转中心移回去，需要旋转的点/向量也会相应的被移动。所以，我们还需要乘上一个平移矩阵才能得到最终结果

矩阵复合变换

我们对一个点或向量的操作肯定不止单单平移或者单单旋转这么简单。通常，在涉及坐标空间的变换时一个向量会旋转并被缩放。当涉及到不止一个矩阵变换时，我们将其称之为复合变换。简单来说，复合变换就是多个变换矩阵相乘，以达到最终效果的过程（需要注意变换顺序）。
在矩阵变换中，我们使用的齐次坐标是列矩阵的形式，乘法的顺序是从右往左。似乎从小到大我们接触的都是从左乘到右的铁律，为什么复合变换我们是从右乘到左呢？原因很简单，首先我们没有违反矩阵乘法的定律，右乘符合结合律。最右边的是我们的点或者坐标，当我们每右乘一个变换矩阵的时候，我们可以马上得到经过一步变换后的点或向量的坐标，这比将所有复合矩阵乘完再乘点/向量要直观的多！如果左乘，我们将再经过复杂的4*4运算之后直接得到结果，万一结果是错的我们也不知道从哪里下手，修改起来会很难。所以为了更加直观，我们举个例子：
如果我们用P指代空间中一点的坐标，用M指代变换矩阵：