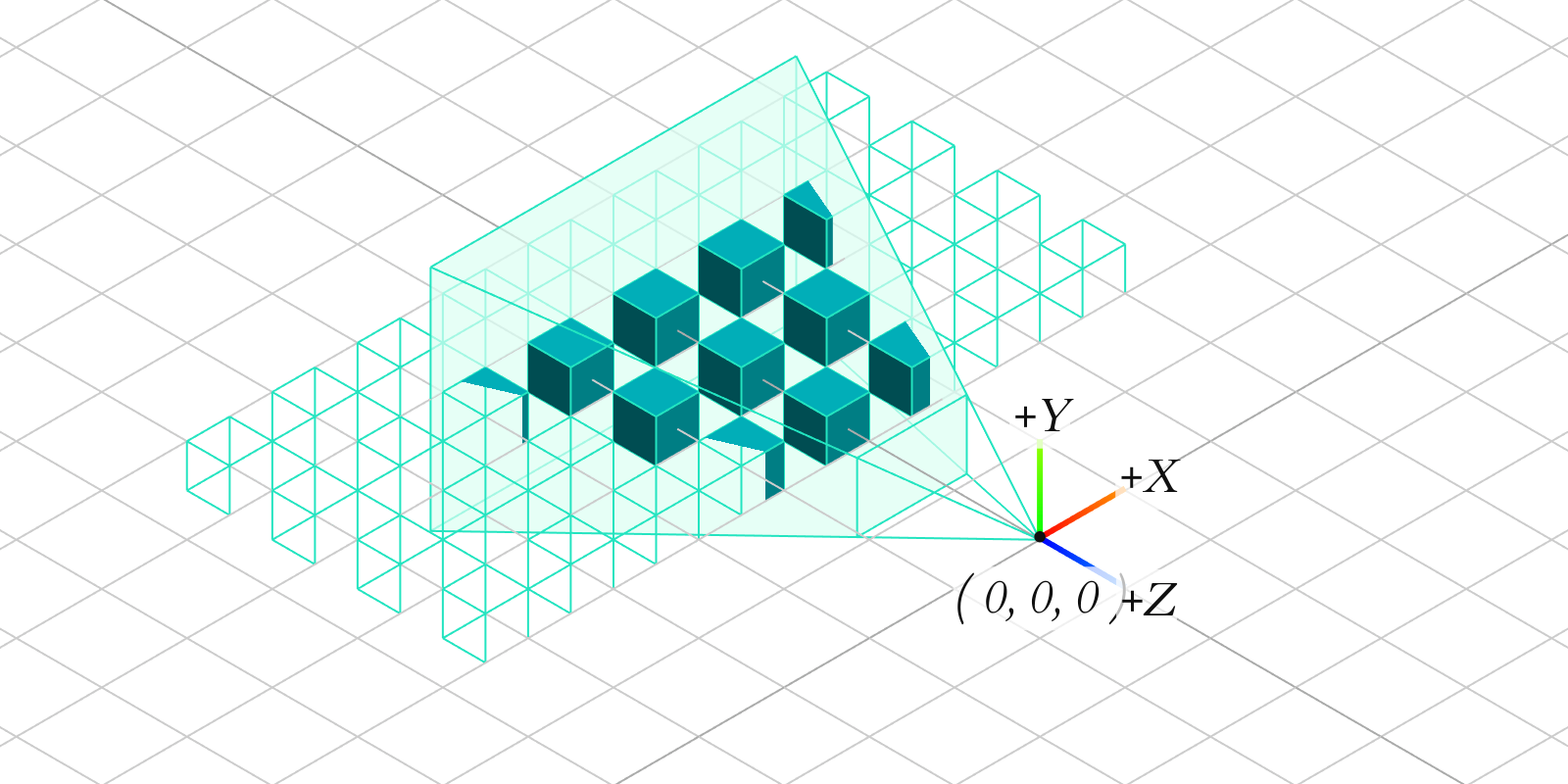
光栅(Raster)这个词最初来源于德语的“屏幕”一词,相当于英语中的Screen。那么光栅化的含义就比较明确了,指的是把图形从标准立方体(NDC)绘制到屏幕上的过程。
屏幕坐标系
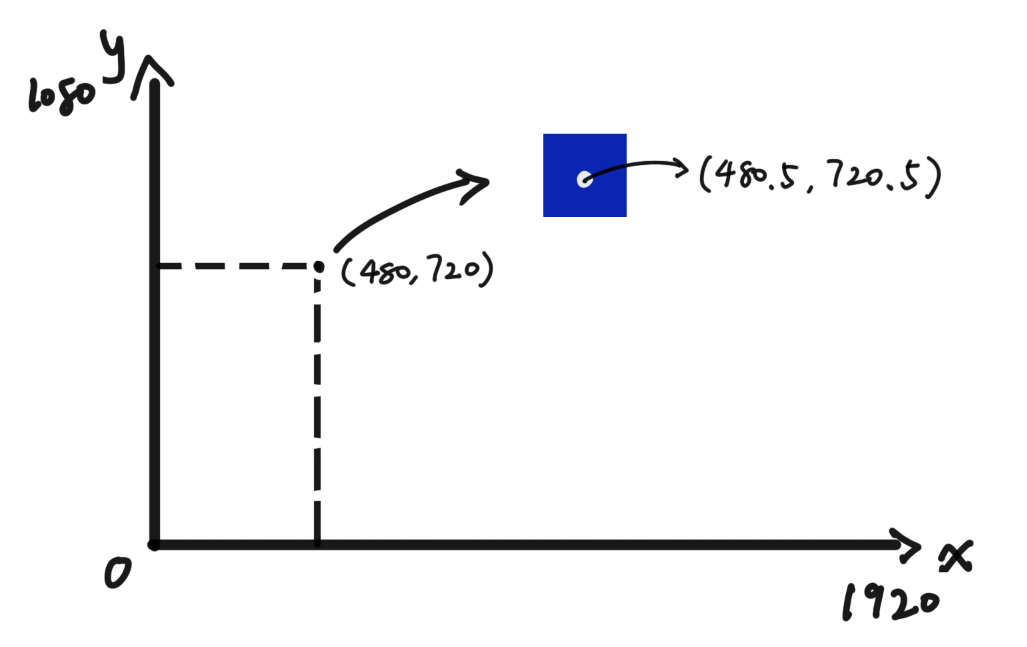
我的笔记本电脑的主显示屏分辨率是1920*1080,代表长1920个像素,宽1080个像素,一共有1920*1080个像素。假设以屏幕左下角为原点建立坐标系,可以给每个像素一个坐标。但由于像素具有实际大小,每个像素的中心点坐标为
从NDC到屏幕坐标系
屏幕映射(Screen Mapping)
NDC是一个长宽高范围均为[-1, 1]的标准立方体。在经过MVP矩阵变换与齐次除法之后,现在要做的就是把具有三维属性的NDC映射到只有二维属性的屏幕空间,怎么实现呢?
如果忽略z(深度信息),其实可以直接把NDC的x和y属性“拉伸”成屏幕空间的形状,使用视口变换矩阵:
所以,NDC内每一点乘以M之后变成了。
好了!现在每个顶点都找到了在屏幕空间中的位置,经过三角形设置与三角形遍历之后就能获得一组片元序列。但是片元终究不是像素,还需要从三角形到像素的转化过程。
采样
离散采样点
如果我们知道一个函数 ,我们可以在 等于不同的数值的时候求出一个对应的结果。这些点是离散而非连续的。
在屏幕空间,我们知道每个像素中心点的坐标是 。假设我们有下图所示的三角形,三角形覆盖范围与各个像素中心点的覆盖关系如右图所示。
标红的部分表示像素中心点在三角形内。从这里可以抽象出一个 函数,在三角形里时返回1,否则返回0,对像素中心点进行采样的过程即一种离散采样的过程。
关于边界问题,如果一个像素的中心点正好在两个三角形的共边上怎么办?通常:
- 一些图形学API(如OpenGL)严格规定了上边和左边上的点属于该三角形
- 不做处理
- 自己做一些特殊处理,比如插值等
inside函数
用inside函数来定义一个点是否在三角形里,那这个函数应该怎么实现呢?
嗯,当然是用叉乘判断点的位置啦。根据叉乘所得到的结果可以判断点在三角形某一边的左侧还是右侧,使用三条边依次进行叉乘判断,就能缺点点是否在三角形内了。
AABB法
呃,不会对每个三角形都要遍历整个屏幕空间吧?如果是真的,现在人们的烧烤方式可能是围在电脑旁。对于所有三角形,我们可以划分出对应的轴向包围盒(AABB)区域,例如下图的蓝色区域:

那么显然,在遍历的时候只需要遍历包围盒内的点信息就好了。
逐行遍历
AABB并不是最好的包围盒,因为当一些物体呈现狭长又旋转了的姿态时,AABB会框住大量无用的部分。对比球包围盒、AABB和OBB:

既然包围盒多少都会携带无用的空区域,我们为什么不直接考虑三角形本身来计算点呢?

抗锯齿

经过采样,给像素着色,我们得到了右图的三角形。
这显然不是我们想要的平滑三角形,而是一个锯齿严重到肉眼可见的怪兽。这表现在:由于空间上的采样率较低(覆盖的像素较少)而导致的信息缺失、走样,或者说失真。
常见的采样问题
- 一张好好的图片,经过压缩之后出现了莫名其妙的摩尔纹
- 锯齿边的问题
除了上面两种因为空间采样率不足的问题(摩尔纹是由于仅采样奇数行列或偶数行列的像素造成的)之外,还存在时域上的采样问题,例如:- 盯着高速旋转的物体,感觉它在“倒转”
这是由于人眼的采样率跟不上信号(运动的物体)变化的速度造成的
我们知道图像其实也是一系列信号,为什么采样率跟不上信号变化速度就会出现“倒转”的问题呢?
通过傅里叶变换,任何一个信号函数 都可以被细分成傅里叶级数 ,例如下图展示了级数的每一项:

如果以上图中的时间间隔采样,到 时就已经难以通过采样点还原函数原本的样子了,想想香农定理:

其中 为最大频率, 为采样频率。 又被称作尼奎斯特频率。当不满足这个条件的时候就会出现错误的视觉效果(aliasing,也就是混叠)了。
思路
预模糊/滤波处理

预模糊(Blur)
在处理有向距离场的锯齿边缘时找到一篇采用预模糊方法处理抗锯齿的不错的博客,可以参考一下:
https://drewcassidy.me/2020/06/26/sdf-antialiasing/

在shaderlab中,可以使用 smoothstep 函数来柔化边缘以实现抗锯齿。
但模糊的本质是————
滤波(Filter)
滤波顾名思义就是过滤掉指定频段的波。以下是两种滤波器的介绍:
 高通滤波器,指的就是“通过高频段,过滤掉低频段”。右图的频谱图中心的黑圈显示了被过滤掉的低频部分。
高通滤波器,指的就是“通过高频段,过滤掉低频段”。右图的频谱图中心的黑圈显示了被过滤掉的低频部分。
 低通滤波器,指的就是“通过低频段,过滤掉高频段”。右图的频谱只保留了中心被留下的部分低频段信息。
低通滤波器,指的就是“通过低频段,过滤掉高频段”。右图的频谱只保留了中心被留下的部分低频段信息。
你有没有发现,高通滤波返回的结果往往是一些边界,低通滤波则返回了模糊?
这是因为边界界定了一种范围的“变化”,划分了两个或多个区域。这代表边界的信号变化更大,频率也更高。而在低通中,高频的“边界”被过滤,留下了模糊的图像。这可以应用在后处理、人脸磨皮中,例如针对高频的线进行拉伸抖动实现运动模糊。
通过设置过滤的频段,可以得到更多不同的效果:

在此基础上加上噪声向上扭曲,就可以制作出人“热的冒烟”的效果。有时间可以试试。
滤波又和卷积有关。卷积是非常常用到的一个的概念,本质上是对一个信号、将相邻的信号与其做加权平均处理的一个过程。可以定义一个卷积核,对像素进行卷积处理,实际上也是一种滤波的形式。卷积让图像更匀称的被模糊,因为对每个像素的处理是一样的。在生成的频域图像里(如下图),可以明显发现图像被过滤了高频。

值得一提的是,将频域图添加到正常图像的a通道中,可以实现一种色图加密。这不难实现,但想想图片文件夹吧的吧主…
使用更好的设备
 如果采用视网膜显示屏,像素更多,采样率更高,就越不会出现混叠问题
如果采用视网膜显示屏,像素更多,采样率更高,就越不会出现混叠问题
几种常用方法
SAA (Supersampling AA)
一般称作超采样,对单个像素进行超分采样,例如在下图的像素中再划分出4*4:

MSAA的计算可以用这样表示:



MSAA的缺点也很明显,那就是过多的细分会导致计算量急剧增加,而且抗锯齿的效果也一般般。提升效果的方法可以是不规则划分细分采样的分布,例如采用随机数。
FXAA (Fast Approximate AA)
快速近似抗锯齿的方法,实现原理与采样无关,而是聚焦于后处理,是最有效的抗锯齿方法之一。
在获得了有锯齿的图像之后,FXAA在后处理中识别到这些包含锯齿的边缘,再修复替换成没有锯齿的边。可以在Unity资源商店里找到:

Unity的Post-Processing模块也包含了FXAA,根据FXAA模型的不同可以获得不同的效果(例如,小模型更快但效果更差,适合移动端)。详细可以参考:https://docs.unity3d.com/Packages/com.unity.postprocessing@2.1/manual/Anti-aliasing.html
- 快速高效
- 不同模型适合不同平台
MSAA (Subpixel Morphological AA)
子像素形态学抗锯齿。SMAA是一种比FXAA更高质量的抗锯齿效果,但相应的它的处理速度也比较慢。SMAA同样也是基于后处理的抗锯齿方法,可以在Unity的Post-Processing模块找到。
- 不支持AR/VR
- 不适合移动端
TAA (Temporal AA)
一篇不错的博客:https://www.sardinefish.com/blog/444
时间性抗锯齿。TAA是一种先进的抗锯齿技术,它也是前文所提到的几种抗锯齿技术中开销最高的。TAA允许帧随着时间的推移积累到历史缓冲区中,以便更有效地平滑边缘。它在平滑运动中的边缘方面有很大的优势,但需要运动矢量,是桌面和控制台平台的理想选择。TAA也是一种基于后处理的抗锯齿方法,可以在Unity的Post-Processing模块找到。
- 不支持OpenGL ES2
- 需要深度纹理和运动向量
- 开销大