基本概念

光源(Light Source)

光从光源中发射出来，照到物体表面。对于不同类型的光，需要设置不同种类的光源（例如影响全局的场景光、点光源以及投射灯等等）。
在Unity中，当我们选择创建光源时，有以下四种选项(反射球暂时先不考虑)：

辐照度(Irradiance)

辐照度是衡量一个光源发出的光的多少使用的单位，用来量化光。

对于平行光，辐照度可以通过计算垂直于光源方向l的单位面积上单位时间内穿过的能量得到。
而存在一定夹角的时候，可以通过求光源方向l和法线之间的夹角的余弦值求得（就是投影到垂直平面的方向的分量）。
当光线间隔相同时，光与平面的夹角越大，单位面积内光的数量越少。

出射度(Exitance)

衡量出射光线的数量和方向的量，利用入射光线的数量和角度计算。和辐照度存在线性关系。

吸收和散射

光与物体相交有两个结果：散射和吸收。

散射(Scattering)
散射只改变光的方向，但不改变光的颜色和密度，如下图：

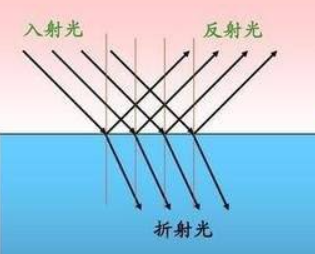
散射分为折射(Refraction)和反射(Reflection)，如上图的两个不同方向的出射光所示。对于不透明物体，折射进入物体内部的光线还会据徐与内部的颗粒进行相交，其中一些光效最后会重新发射出物体表面，而另一些则会被物体吸收。反射则在物体表面直接被弹出来了，但是如果物体表面粗糙会往不同的方向进行反射。
针对反射的两种性状，我们有漫反射(Diffuse)模型与高光反射(Specular)模型。

吸收(Absorption)
吸收只改变光线的密度和颜色，不改变光线的方向。也就是说，吸收将光的能量吸收走了，而散射并没有只是改变了光的方向。

graph LR
  光与物体相交 --> 散射
  光与物体相交 --> 吸收
  散射 --> 折射
  散射 --> 反射
  反射 --> 漫反射
  反射 --> 高光反射

着色(Shading)

着色指的是根据材质属性、光源信息去使用一个或多个等式计算沿某个观察方向的出射度的过程。这些等式就是“光照模型(Light Model)”

标准光照模型

标准光照模型只关注直接光照(Direct Light)，也就是从光源出发，照射到物体表面，反射回摄像机的光线。于是，我们可以称标准光照模型为局部光照模型。
进入摄像机的光线(符号：c~光线类型~)往往分为以下四种：

漫反射(Diffuse)

兰伯特模型（Lambert）

用于描述当光线照射到物体表面，物体表面会向每个方向散射多少辐射量。对于漫反射而言，观察角度并不重要，因为我们默认漫反射在各个方向的分布是一样的。但是入射光线非常重要。
漫反射符合兰伯特定律(Lambert’s law)：

c_{diffuse} = (c_{light} \cdot m_{diffuse})max(0, \hat{n} \cdot \hat{l})

其中， $\hat{n}$ 为法线向量(normal vector, 一般用n表示)， $\hat{l}$ 为光源的单位矢量， $m_{diffuse}$ 就是材质的漫反射颜色， $c_{light}$ 是光源颜色

半兰伯特模型（Half Lambert）

漫反射可以有逐顶点和逐片元两种模型(均满足兰伯特定律)，但是它们的暗部都是全黑的，这使得从暗部观察物体时不利于细节呈现并且看起来像个平面。通过更改兰伯特定律公式，我们可以得到半兰伯特模型的漫反射计算公式：

c_{diffuse} = (c_{light} \cdot m_{diffuse})(\alpha (\hat{n} \cdot \hat{l}) + \beta)

与兰伯特模型不同的是，半兰伯特模型对法线和光源的点乘进行的一个缩放并偏移。通常， $\alpha$ 与 $\beta$ 的值均为0.5，可以将光与法线的点积映射到[0, 1]范围中。
三种方式计算漫反射背光部分的差别：

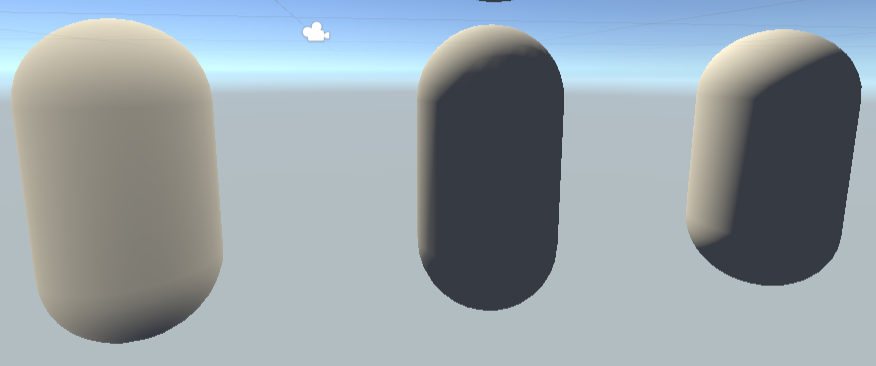
三种计算漫反射的方式(左：逐像素；中：逐顶点；右：半兰伯特)，可以看出逐顶点漫反射有明显的锯齿边

高光反射(Specular)

用于描述当光线照射到物体表面，物体表面会在完全镜面反射方向散射多少辐射量。
高光反射需要知道四个向量的值，即人眼观察方向(v)、法线方向(n)、光源方向(入射光l)、反射方向(出射光r)。

Phong模型

Phong模型和物理中的光学模型类似，主要特征是入射光 $\hat{l}$ 、出射光 $\hat{r}$ 和法线 $\hat{n}$ 的夹角相同。出射光 $\hat{r}$ 的计算公式为：

\hat{r} = 2(\hat{n} \cdot \hat{l}) \hat{n} - \hat{l}

高光反射光的计算公式为( $m_{gloss}$ 为材质光泽度，值越大材质光斑越小。max的作用是防止负数出现，避免背后的光照亮物体)：

c_{specular} = (c_{light} \cdot m_{specular})max(0, \hat{v} \cdot \hat{r})^{m_{gloss}}

Blinn-Phong模型

Blinn-Phong模型对Phong模型进行了简化，引入了一个新的矢量 $\hat{h}$ 代替反射光线。 $\hat{h}$ 是对 $\hat{v}$ 和 $\hat{l}$ 取平均再统一化得到的，指的是v和l中间的向量：

\hat{h} = \frac{\hat{v} + \hat{l}}{\vert \hat{v} + \hat{l}\vert }

高光反射光的计算公式为: $$c_{specular} = (c_{light} \cdot m_{specular})max(0, \hat{n} \cdot \hat{h})^{m_{gloss}}$$

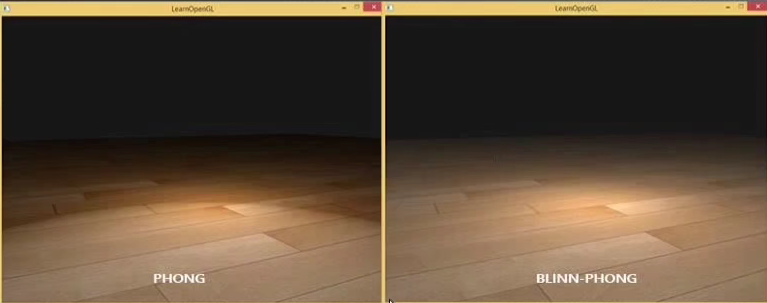
当摄像机无穷远时，我们认为 $\hat{v}$ 和 $\hat{l}$ 均为定值，此时 $\hat{h}$ 为定值，使用Blinn模型的速度将更快。而当 $\hat{v}$ 和 $\hat{l}$ 处在变化之中时，Phong模型更占优势。此外，一些适合Blinn模型更符合实验结果。因此具体选择哪种攻击计算高光反射需要依效果而定。比如当入射光方向和人眼观察方向在法线的同一侧时，Phong模型会产生奇怪的日食状“断层”现象，而Blinn-Phong模型则不会：