为什么要单独说说map和Dictionary呢?因为这两个容器非常经典也很常使用到。对于一个开发者来说,了解它们如何实现是有必要的,官方文档中对二者的定义如下:
map用于存储和检索集合中的数据,此集合中的每个元素均为包含数据值和排序键的元素对,大小可变。
键的值是唯一的,用于自动排序数据。可以直接更改映射中的元素值。键值是常量,不能更改。
必须先删除与旧元素关联的键值,才能为新元素插入新键值。
map是可逆的,因为提供了双向迭代器来访问其元素。
1 | template <class Key, |
其中Traits代表了自动排序的规则(默认为less),Allocator则是一种表示存储的分配器对象的类型(默认对,pair)。
dictionary表示键和值的集合,是一个泛型集合,它以不特定的顺序存储键值对。
字典不能包含重复键 或 null键,而值可以是重复键或null键。键必须是唯一的,否则将引发运行时异常。
1 | public class Dictionary<TKey,TValue> : |
从文档的介绍来看,map 和 dictionary 都是存放键值对的大小可变的容器,不同的是 map 是有序的而 dictionary 是无序的。为什么一个容器有序而一个无序呢?这要从这两种容器底层的数据结构说起。
底层数据结构
map的底层是红黑树,这是一种特殊的自平衡二叉搜索树(Balanced Binary Search Tree),其中插入、删除、搜索的时间复杂度均为指数级的 ,且由于其特殊规则而不会像普通的二叉搜索树(BST)那样退化成链表,是一种效率极高(特别是插入和删除)的二叉树。
dictionary的底层则是耳熟能详的哈希表,是一种散列表,通过哈希函数来计算键的哈希值并决定将键值对存放在哪个位置。
红黑树
红黑树是具有以下性质的特殊二叉树:
- 节点只有两种颜色,红色和黑色
- 根节点一定是黑色的
- 红色节点的父节点和子节点必须是黑色的
- 从当前节点(包括它本身)出发走到nil,不论哪条路径所经过的黑色节点数目相同
在数据量庞大的时候,红黑树依然能快速搜索出想要寻找的元素,而且它是自平衡的二叉搜索树。在规则被打破时,红黑树通过重新着色和旋转(分为左旋、右旋、左右旋、右左旋)的方式实现自平衡。红黑树插入和删除效率更高的原因是旋转的次数更少。AVL树是“严格平衡”的二叉搜索树,需要更多的旋转来调整;红黑树只保证了“黑平衡”(从任意节点出发到叶子节点经过的黑点数量相同,但经过的红节点数量不确定,最差的情况下经过的红节点和黑节点一样多),是以牺牲部分搜索性能换取增删性能的折中方案,用非严格的平衡换取旋转次数的减少。
在C++中,std库底层默认通过less than(<)比较各个元素,将节点落于红黑树中的正确位置。开发者也可以自定义比较器(比如改成>)更改键的排序规则。对于一颗二叉搜索树,其中序遍历的结果就是有序的。
对于C++中的string,由于默认的string是系统的xstring对象没有定义
<操作符,因此需要开发者自行定义一个。
因为map的迭代总是有序的,所以它适合需要有序存储或按范围查询的场景。在实际使用中,如果所维护的树需要频繁增删节点,红黑树会更加合适。在频繁按键查找元素的场景下,map并没有dictionary优秀,原因会在下一小节给出。
哈希表
在介绍C# Dictionary方面有一篇非常好的文章,我在此仅作一些归纳总结。
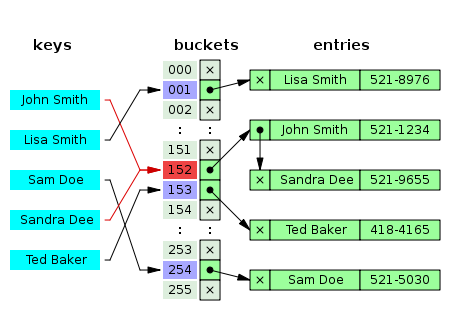
哈希表是一种散列表,其中的数据是无序的。在将一个数据(键值对,即entry)存入哈希表时,会发生下面的步骤:
- 将键(key)输入哈希函数中,计算出哈希值(hash value)
- 根据哈希值和哈希桶算法确定键值对应该被放入哪个桶(bucket)中
- 如果桶中已经有元素了,利用碰撞处理方法解决碰撞(冲突)
- 当频繁碰撞或桶满了,需要对哈希表进行扩容,执行rehash
哈希表搜索的时间复杂度是 ,因为每个元素都有对应的key值,直接抓出key值就是对应元素了。
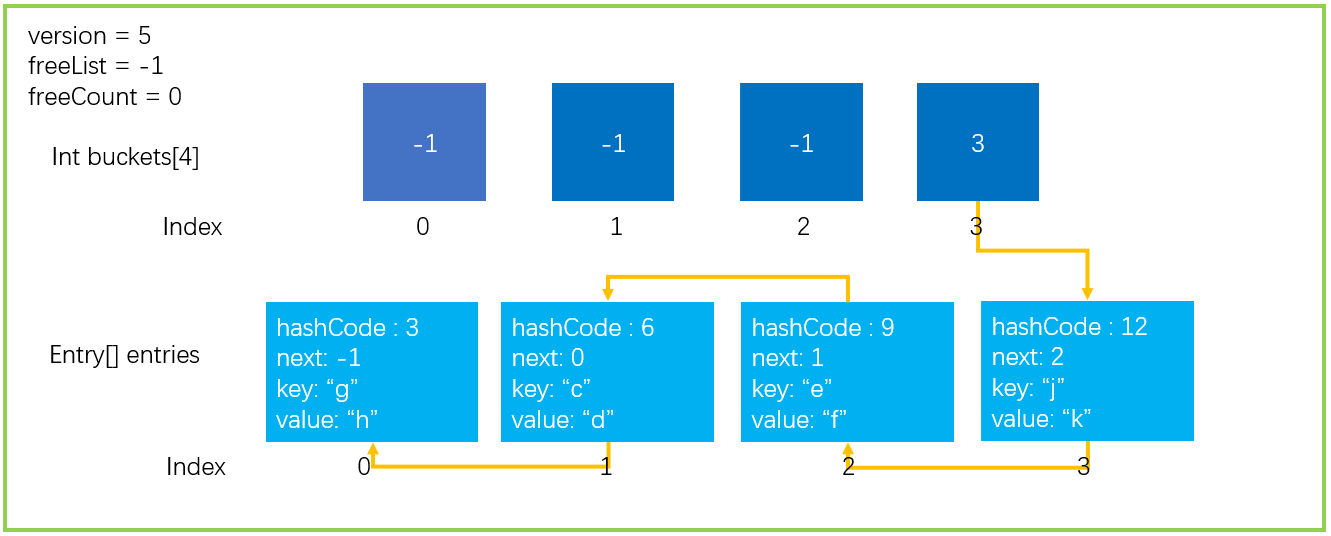
entry
Entry是一个结构体,它的定义如下代码所示。这是Dictionary种存放数据的最小单位,调用Add(Key,Value)方法添加的元素都会被封装在这样的一个结构体中。
1 | private struct Entry { |
我们遇到了不少名词,下面将详细介绍一下。
哈希函数

哈希函数是一种摘要算法(把消息或数据压缩成摘要,使得数据量变小),具有幂等性,且不可逆(无法通过哈希值逆推键),不同的键通过哈希函数可能计算出相同的哈希值,这也为之后的冲突埋下了伏笔。一个好的hash function应该具有以下几种功能:
- 容易计算
- 均匀分布
- 减少碰撞
常见的哈希函数有直接寻址法、平方取中法、折叠法、随机数法、除留余数法(这也是常在题目中出现的哈希函数)等。
哈希桶算法
经过哈希函数计算出的哈希值可能非常大,而实际上哈希表并没有那么多桶和这些哈希值一一对应。为了能把哈希值映射到桶里,哈希桶算法会对哈希值取余数。
桶的数量和哈希表的容量有关,未指定具体初始大小时C#默认的哈希表大小为4。
哈希冲突与解决方法
当两个不同的键通过哈希函数与哈希桶函数的计算后得到的结果一样时,就代表发生了碰撞,两个键值对被指向了同一个桶,这就是哈希冲突。常见的解决方法有拉链法(这也是Dictionary采用的)、开放定址法、再Hash法等。
拉链法也叫链式冲突解决法,这种方法的思路是将产生冲突的元素建立一个单链表,并将头指针地址存储至Hash表对应桶的位置。这样定位到Hash表桶的位置后可通过遍历单链表的形式来查找元素。
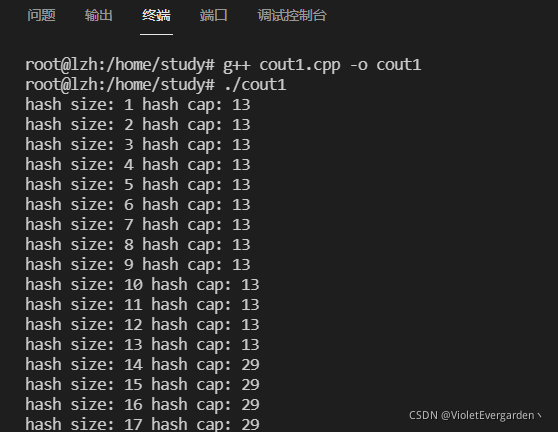
满表扩容
当哈希碰撞次数到达一个阈值(100次)或者哈希表满了的时候会触发扩容操作。在C# dictionary的扩容中,
- 申请两倍于现在大小的buckets、entries
- 将现有的元素拷贝到新的entries
- 如果是因为达到碰撞阈值扩容,使用新哈希函数重新计算Hash值
虽然换了新的哈希函数,但仍可能发生大量哈希碰撞。在JDK中,HashMap如果碰撞的次数太多了,那么会将单链表转换为红黑树提升查找性能。不过目前.Net Framwork中还没有这样的优化。
unordered_map?SortedDictionary?
C++中对于键值对的存储还有一种实现—— unordered_map。它与C#的 dictionary 类似,是通过哈希表实现的。
unordered_map 相较于 dictionary 的一些区别是:
- 哈希碰撞时采用开地址法
- 不同编译器下的扩容规则不同,有8/2.x倍扩容的

SortedDictionary是C#中对map的方案,底层同样也用了红黑树。由于排序的存在,它的各项性能其实并不如Dictionary。
参考资料
https://learn.microsoft.com/zh-cn/cpp/standard-library/map-class?view=msvc-170
https://learn.microsoft.com/zh-cn/dotnet/api/system.collections.generic.dictionary-2?view=net-9.0
https://www.cainiaoplus.com/csharp/csharp-dictionary.html
https://www.cnblogs.com/InCerry/p/10325290.html
https://blog.csdn.net/jingyi130705008/article/details/82633778
https://zhuanlan.zhihu.com/p/95892351



